Graph theory is the study
of graphs, those
are mathematical structures used to model pairwise relations between objects. A
graph in this context is made up of some nodes, branches, or points which are
connected by edge, corners, arcs,
or lines. A graph may
be undirected, meaning
that there is no distinction between the two vertices associated with each
edge, or its edges may be directed
from one vertex to another vertex.
Graph
it is the collection of nodes and branches of network.
|
|
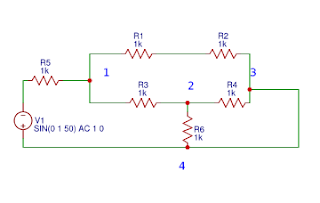
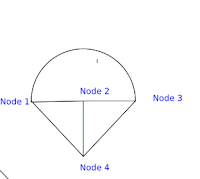
If we observed the above
circuit diagram we will see four nodes. Those are represented as a 1, 2, 3
& 4. In fig (b) represented as the equivalent graph diagram of fig (a).
INCIDENCE MATRIX
a branch whose end fall on node is called
incident branch
 |
| Incidence Matrix |
With the help of the above fig it is clearly
understand that what an incidence branch is? As definition of incidence branch
in the above fig. 1 & 2 are incidence branches because those currents are
end fall (current is towards node) at node .so, those two reference branches
are incidence branches.
Rank of graph
·
Rank = (n-1) n=nodes
·
No.of KCL
eq’n = (n-1).
TREE
The collection of minimum no. of branches
connecting all the nodes of a graph without making a loop.
 |
| Electronic Circuit Representation Graph |
For example let us see detailed
explained of tree with the help of above diagram. In the above graph there are
six branches are there. On those six branches 2, 5 & 6 forms the tree.
Because tree never contain loop.
Now you will get one dought i.e. why we should take only 2, 5, & 6
and also why we should not take all or 1, 3 & 4. Because as the definition tree never contain loop. That’s why we
should take only 2, 5, 6 only.
The below fig shows the tree graph. I hope
you will be understand if you see this fig.
 |
| Tree Representation Graph |
·
A
single graph has no. Of trees
· The no. Of trees: nn-2
· The
above formula can be applicable only if all nodes are interconnected.
·
A tree never contain loop
TWING
Branch of tree is called “twing”
Based on the definition of twing in the above
fig 2, 5 & 6 branches are Twings (Twing is branch of tree remember it .).
COTREE
Remaining part of a graph after removal of Twings is called co-tree
It is a collection of links.
 |
| Co-Tree Representation Graph |
LINK
Links are branches. these are nothing but all
the branches remove from the graph to make a Co-tree.
Here 1, 3, 4 are Links
·
The
total no. Of branch of graph’s are we can find using these following formula
B = (n-1) + l
· No of twings = (n-1) = no. Of KCL eq’n
·
No. Of
loop’s = no. Of links