Oscillators | RC Phase Shift | Wien Bridge | Crystall Oscillators

Oscillators is device or circuit it can produce a continuous wave from without giving any  input to that.

In oscillator oscillations are produced by satisfying the conditions of barkhausten criterion to sustain the frequency of oscillations.

·       The loop gain i.e. Aβ must be equal to ‘1’  ( Aβ = 1)

·       But practically it is slightly greater than are equals to 1  (Aβ ≥ 1)

·       The total phase shift introduced must be zero or integral multiplies of 2π.

We have following types of oscillators are there. Those are

·       RC phase shift oscillators

·       Wein bridge oscillator

·       LC oscillator

·       Hartely oscillator

·       Colpitts oscillators

·       Crystal oscillators

RC-PHASE SHIFT OSCILLATORS:

  

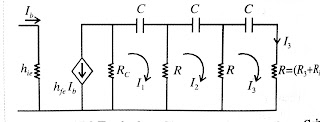
 In RC-phase shift oscillators having three RC combinations in it’s feedback path Each RC combination can produce 60⁰ phase shift so overall 180⁰ produces. In order to satisfy barkhausten criterion, forward path consisting of a inverting amplifier which also provides the phase shift of another 180⁰ phase shif.

  Then the total phase shift around the circuit is 360⁰ the below fig shows the simple RC phase shift network

   The above fig shows the feedback path of RC-phase shift Oscillator.

                                        The above fig shows the negative feedback RC-phase shift oscillator. Because, feedback path is connected to negative terminal in order to get 180⁰ phase shift.

·       W₀ = 𝟏/ 𝑹𝑪√𝟔     

·       F₀ = 𝟏/ 𝟐𝝅𝑹𝑪√𝟔

·       β  = -1/29

·       forward path gain A= -R_f / R

By barkhausten criterion

·       |A β | ≥ 1

·       (-R_f / R) * (-1/29) ≥ 1

       

RC – PHASE SHIFT OSCILLATOR USING BJT

  

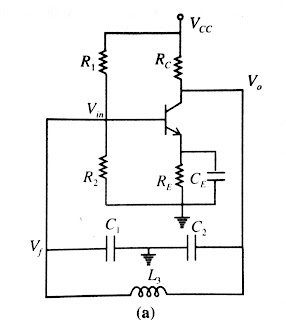
    CE amplifier is an inverting amplifier which can be used to construct phase shift oscillator as shown in below. The feedback voltage is used as a Voltage Shunt Feedback

                         In the above circuit biasing resistors R₁ & R₂ are very large.which makes the input resistance of CE is very high. The transistor is replaced by simplified model with the assumption that h_oeR_c≤ 0.1. the resistor R= R₃ + R_in

                           

The frequency of oscillations are given by    For made up of BJT oscillators

·       w₀ = 𝟏/𝑹𝑪√𝟔+𝟒 𝒌 

·       F₀ = 𝟏/ 𝟐𝝅𝑹𝑪√𝟔+𝟒 𝒌           ( k = Rc / R )

·       K value is approximately =  2.7

·       (h_fe)_min = 44.5

·       

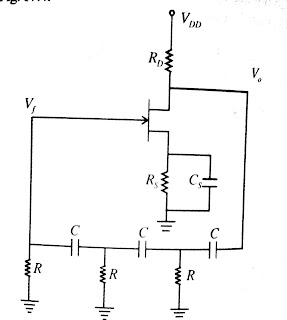
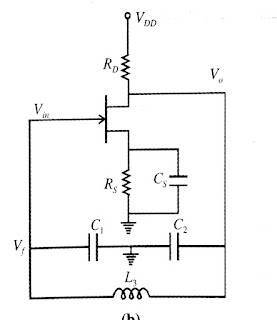
   RC – PHASE SHIFT USING FET

            Common source amplifier is a inverting amplifier which can be used to construct a phase shift oscillator as shown in fig.

    

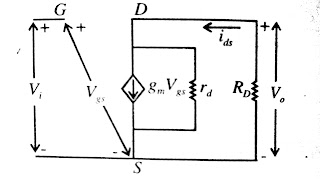
    The JFET phase shift oscillator uses the RC phase shift feedback network described. The frequency of oscillations is w₀ = 𝟏/𝑹𝑪√𝟔. The forward path gain of amplifier can be obtained by the ac analysis of common source transistor. In CS  ac analysis of amplifier source capacitance C_s is short circuited and JFET is replace by small signal equivalent diagrams as shown in below fig.

·       Output voltage V₀ = (-g_mr_dR_DV_i ) / (R_D + r_d)

·       Trans conductance g_m = 29 / R_D

·       Voltage gain A_v = (V_o  / V_i )

                       =  (- g_mr_dR_D) / (R_D + r_d)

·       If  r_d less than R_D

A_v  = -g_mR_D

·       β = -1/29

·       f0 = 𝟏 / 𝟐𝝅𝑹𝑪√𝟔

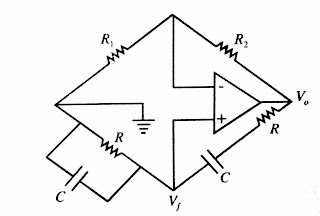
Wien bridge oscillator:

Non-inverting op-amp  in forward path and RC n/w in the feedback path form a wien bridge oscillator as shown in below fig.

At frequency of oscillator RC n/w in feedback path will not produce any phase shift.

·  Wien bridge oscillator produces 10HZ to 1MHZ range of frequencies.

· Wien bridge oscillator having both positive feedback & negative feedbacks.

· Wien bridge oscillator generates zero 0⁰ phase shift oscillations.

The below fig shows the wien bridge oscillator

·       Feedback factor of wien bridge oscillator is          
     β = (R₂C₁) / (R₁C₁ + R₂C₂ + R₂C₁)

·     Lower cutoff frequency of wien bridge oscillator                                 F_L = 1/(2πR₂C₁)

· Higher cutoff frequency of wien bridge oscillator                    

                         F_H = 1/(2πR₁C₂)

·       F₀ = 1/(2π√(R₁C₁ + R₂C₂ )

·       β = 1/3

·       A=(1+ R₂ / R₁)

·       A β ≥ 1

·       R₂ ≥ 2R₁

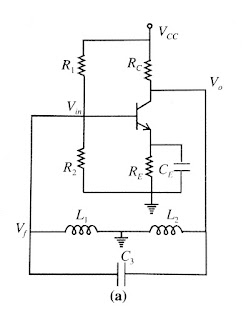
Collipt’s Oscillator’s

  Collipt’s oscillators’ fig is as shown in below fig.

Fig.a) using BJT

Fig.b) using FET

·       F =  1/(2π√(LC_T )

·       C = C₁C₂ / (C₁ + C₂)

·       β = C₁ / C₂

·       A_Vmin = 1/β = C₂ / C₁

HARTELY OSCILLATOR

·       F =  1/(2π√(LC_T )

·       C = L₁ + L₂ + 2M

·       β = L₂ / L₁

·       A_Vmin = -1/β = L₁ / L₂

·       If they gave mutual  inductance the A_Vmin is changed.

A_Vmin = 1/β = (L₁+M) / (L₂+M)

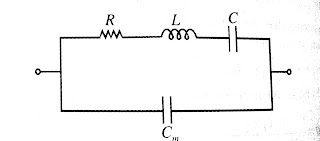
Crystal Oscillators:

            Crystal oscillators full fill the criteria of food accuracy and stability of the frequency of oscillations. Quartz crystals are used for Crystal oscillators which exhibit the piezoelectric effect.  When ac voltage is applied to the across the Crystal it vibrates at a frequency of applied voltage. Conversely if it is vibrated it generates an ac voltage of frequency same as the frequency of vibration. Quartz Crystal symbol and circut model as shown in below. 

    A Quart crystal is mounted between two metallic plates which results in mounting capacitor connected in parallel with series RLC connection in circuit model. 

                    

                                        

·       Rochellist has excellent piezoelectric effect. But , it has poor mechanical strength.

·       Tourmaline has poor piezoelectric effect. But, it has excellent mechanical strength.

·       So we use quartz. Quartz has good capabilities of those both.

OSCULLATORS