Series Resonance | Series RLC Resonance Circuit

Introduction:

                   At resonance the impedance of the circuit is real i.e. means purely resistive only. This occurs because the reactance of inductor and capacitor at resonance are equal but oppositive sign and cancel out each other.

        In this topic we will see what is resonance and resonance types i.e. series resonance, parallel resonance.

And also we will discuss from important formulas of this resonance.

What is Resonance?

                          We will know what is resonance with the help of this following circuit diagram.

                                     

                  

  In electric circuit resonance is nothing but a phenomenon at which the response of the circuit is maximum for a given particular frequency.

              Let us consider the above fig is formed with resistor, capacitor, and inductor. AC input voltage with particular frequency is applied to the circuit. Now assume these input voltage is variable voltage.

As we applied to the input voltage to circuit we will some output at output terminals. And then we will tune or varies the input voltage with frequency the maximum output we will get at some frequency. This phenomenon in electronic circuit is known as the Resonance. The frequency at which we will get maximum response is known as the “Resonant frequency”.

                 Now we will about resonance through these following LC circuit.

     

            

                         In the above fig we will know this is the simple LC resonance circuit. This is formed by inductor and capacitor with a voltage source.

                  Now coming to explanation of LC resonance circuit assume that at time t=0 those circuit is connected to short-circuit terminal instead of input voltage (base on initial conditions). This capacitor & inductor both are energy storage devices. And according to their property they don’t respond immediate actions after removing to input voltage circuit.

                Capacitor will be charged when it is charged then ready to discharge through inductor. These causes’ energy will transferred b/w inductor and capacitor. The rate of energy transferred is depends on the values of both inductor and capacitor. This transfer of energy causes oscillations will generate. These oscillations will generate continuously until resistor is introduced.

Even there is no resistance in the circuit but inbuilt in any circuit having some resistance these causes reduced the oscillations. Because resistor dissipated some energy these cause oscillations will reduced and will be disappear. So, we obtain oscillations we need some input voltage to the circuit with same frequency so these oscillations will continue forever.

                     It is the condition when the voltage across the circuit becomes in phase with the current supplied to the circuit.

                            At resonance, the circuit behaves like a resistive circuit. Power factor of a circuit at resonance is become one (1).

Series Resonance Circuit: 

   Now we will discuss about series resonance circuit. Series resonance circuit is shown in below fig.

                                  

                      

  In the series resonance circuit has input voltage source, resistor, capacitor, and inductor. Capacitor and inductor causes oscillations will generate and resistor cause decrease the oscillations. Suppose some input voltage V_i = sinΩt is applied to the circuit at a particular frequency maximum output current we will get
X_L = X_C

ω_L= 1/ω_C 

ω_L* ω_C = 1

ω =1/(√(LC))

f    = 1/ 2Π√LC

at resonance 
 f=f₀ & ω= ω₀

ω₀ =1/(√(LC))

f₀ = 1/ 2Π√LC

I₀=-V/(square root(R²+(X_L-X_C)²)

The graph of series resonance circuit is show in below fig.

                               

                                       

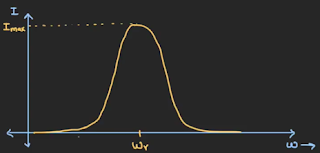
                                           In series resonance circuit at lower frequency range low current will flow through the circuit and also same as at higher frequencies also. At particular frequency the current suddenly increase the maximum range until it will be in that particular frequency. After that it will decrease to zero. 

Because at resonance the current will follow only resistance only. One will see theoretical explanation of circuit

    At resonance       

     Z = R  only  

          X_L = X_C

                                  Impedance is due to resistance only. Because capacitive and inductor reactance are cancelled at resonant frequency.

At lower frequency ranges   X_C = 1/ωc = ∞   C=0 at initial (lower frequencies). So capacitor will acts as open circuit because capacitor reactance is infinity at lower frequencies. So we will not find any current at this lower range of frequencies.

At higher frequencies

                     Inductor reactance (X_L = ωL= ∞) is infinity at higher frequency. So, inductor acts as open circuit at higher frequency ranges and no current will follow through circuit.

In series RLC resonance circuit has some selectivity. This will causes to series RLC resonance used in radio communication engineering. Based on series RLC resonance circuit tune the particular frequency by changing the capacitor value it will   cause shift the resonant frequency  we will get our desired channel.

                      For good selectivity we should be as much as low resistor value. If the resistance is large the shape of output current will be border if we reduced to low value we will get sharp response of output current.

 The selectivity of series resonance circuit is depends on two parameters. Those are

1.     Quality factor

                                                     
2.  Bandwidth

Quality factor:

                          Quality factor is defined as the ratio of Reactive power to active power of resonance circuit.

                             (Or)

 It is also defined as the using these below formula.

  = 2π * (maximum energy stored / energy      dissipated per cycle)

 In the above formulae 

active power = (I_M²R /2)

 Reactive power =(I_M²X /2)

Therefore quality factor of resonance circuit we will find using these following formulas.

Quality factor: 
Q_C= Q_L= (1/ω₀C)

= ω₀L/R

= 1*(√L/C)÷R

At resonance the voltage across the capacitor & inductor are equal to “Q” times the applied voltage.

   Q₀= f₀ ÷ (∆f)

For larger values of quality factor having less bandwidth.

Selectivity:

                      Selectivity of resonance circuit is defined as the ratio of resonant frequency to bandwidth.

Selectivity =
F₀÷ BW (bandwidth)

 = F₀÷ (F_H - F_L)

                       The more selectivity resonance circuit having less bandwidth. ∆F varies inversely propos anal to Q₀.

Bandwidth of series resonance circuit:

Bandwidth of resonance circuit is defined as the difference between the -3-db frequencies in the given circuit.

Also defined as the deference between frequencies at the half power point. 

                      

Band width is difference between higher cutoff frequency (f_H)to lower cutoff frequency(f_L).

Bandwidth = F_H - F_L. after that theoretical explanation we will get bandwidth   

  ω_H - ω_L= R/L

   f_H - f_L= R/2πL

If resistance of circuit is increases the values of bandwidth is increased. These are directly proposinal to each other.

Important points of series resonance circuit:

If ω ˂ ω₀ then series resonance circuit behaves like a RC Capacitive circuit.

If ω ˃ ω₀ then series resonance circuit behaves like a RL Inductive circuit.

If ω = ω₀ then series resonance circuit behaves like Resistive circuit.

At resonance current(I) is maximum and impedance(Z) is minimum.

Simple circuit limits of series RLC Resonance Circuit

Simple circuit	R	L	C	XL=ωL	XC=ωC
Purely resistive	R	0	infinity	0	0
Purely inductive	0	L	infinity	XL	0
Purely capacitive	0	0	XC	0	XC

  the below table shows the phase angle & impedance limits of series resonance circuit.    

                         

Transfer function of series RLC resonance circuit

Transfer function H(s) = V₀(s) / V_S(s)

= R/(R+Ls+(1/Cs))

The characteristics equation is = R+Ls+(1/Cs)

RCs+ LCs² +1 =0

The characteristics equation for second order circuit is

S²+2ζω₀s+ ω₀² = 0

ω₀² = 1/LC

2ζω₀ = R/L

2ζ(1/LC) = R/L

Damping ratio ζ = (R/2)* square root(C/L)

Quality factor is Q= 1/ 2ζ

Bandwidth (Bw) = 2ζω₀ = R/L

Important formulas on series resonance circuit:

_·  At resonance X_L= X_c

_· Resonance frequency f₀    = 1/ 2Π√LC

_·  At resonance  I = V/Z   (Z = R)

_·  V_L= I₀*X_L ,           V_C = I₀* X_C

_·Variation of frequency w.r.t capacitor voltage (V_c)                      

                       

_·       Variation of frequency w.r.t inductor voltage (V_L)         

           

_· If R is extremely small then f_L & f_C tends to equal to f₀.

_·  Selectivity with variable capacitance 
C₀ / (C­₂ – C₁)  = Q₀ / 2

C­₂ – C₁ gives total variation in “C” at half power points. Quantity C₀ / (C­₂ – C₁) is selectivity of tuned circuit with C variable and it is equal to Q₀ / 2.
_·Selectivity with variable inductance
(L₂ – L₁)/L₀ = 2/Q₀

Related topics

PN-Junction Diode

TUNNEL DIODE

                                     

 OSCILLATOR's

 Tree Tieset out set

  DUALITY

  MULTIVIBRATOR

  RESONANCE